Private information retrieval
In cryptography, a private information retrieval (PIR) protocol allows a user to retrieve an item from a server in possession of a database without revealing which item she is retrieving. PIR is a weaker version of 1-out-of-n oblivious transfer, where it is also required that the user should not get information about other database items.
One trivial, but very inefficient way to achieve PIR is for the server to send an entire copy of the database to the user. In fact, this is the only possible protocol that gives the user information theoretic privacy for their query in a single-server setting. There are two ways to address this problem: one is to make the server computationally bounded and the other is to assume that there are multiple non-cooperating servers, each having a copy of the database.
The problem was introduced in 1995 by Chor, Goldreich, Kushilevitz and Sudan[1] in the information-theoretic setting and in 1997 by Kushilevitz and Ostrovsky in the computational setting.[2] Since then, very efficient solutions have been discovered. Single database (computationally private) PIR can be achieved with constant (amortized) communication and k-database (information theoretic) PIR can be done with 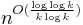 communication.
communication.
Contents |
Advances in computational PIR
The first single-database computational PIR scheme to achieve communication complexity less than  was created in 1997 by Kushilevitz and Ostrovsky [2] and achieved communication complexity of
was created in 1997 by Kushilevitz and Ostrovsky [2] and achieved communication complexity of 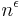 for any
for any  , where
, where  is the number of bits in the database. The security of their scheme was based on the well-studied Quadratic residuosity problem. In 1999, Christian Cachin, Silvio Micali and Markus Stadler [1] achieved poly-logarithmic communication complexity. The security of their system is based on the Phi-hiding assumption. In 2004, Helger Lipmaa [3] achieved log-squared communication complexity
is the number of bits in the database. The security of their scheme was based on the well-studied Quadratic residuosity problem. In 1999, Christian Cachin, Silvio Micali and Markus Stadler [1] achieved poly-logarithmic communication complexity. The security of their system is based on the Phi-hiding assumption. In 2004, Helger Lipmaa [3] achieved log-squared communication complexity 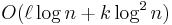 , where
, where 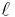 is the length of the strings and
is the length of the strings and  is the security parameter. The security of his system reduces to the semantic security of a length-flexible additively homomorphic cryptosystem like the Damgård–Jurik cryptosystem. In 2005 Craig Gentry and Zulfikar Ramzan [2] achieved log-squared communication complexity which retrieves log-square (consecutive) bits of the database. The security of their scheme is also based on a variant of the Phi-hiding assumption. All previous sublinear-communication computational PIR protocol required linear computational complexity of
is the security parameter. The security of his system reduces to the semantic security of a length-flexible additively homomorphic cryptosystem like the Damgård–Jurik cryptosystem. In 2005 Craig Gentry and Zulfikar Ramzan [2] achieved log-squared communication complexity which retrieves log-square (consecutive) bits of the database. The security of their scheme is also based on a variant of the Phi-hiding assumption. All previous sublinear-communication computational PIR protocol required linear computational complexity of 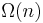 public-key operations. In 2009, Helger Lipmaa [4] designed a computational PIR protocol with communication complexity
public-key operations. In 2009, Helger Lipmaa [4] designed a computational PIR protocol with communication complexity 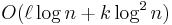 and worst-case computation of
and worst-case computation of 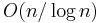 public-key operations. Amortization techniques that retrieve non-consecutive bits have been considered by Yuval Ishai, Eyal Kushilevitz, Rafail Ostrovsky and Amit Sahai [3].
public-key operations. Amortization techniques that retrieve non-consecutive bits have been considered by Yuval Ishai, Eyal Kushilevitz, Rafail Ostrovsky and Amit Sahai [3].
As shown by Ostrovsky and Skeith,[5] the schemes by Kushilevitz and Ostrovsky [2] and Lipmaa [3] use similar ideas based on homomorphic encryption. The Kushilevitz and Ostrovsky protocol is based on the Goldwasser–Micali cryptosystem while the protocol by Lipmaa is based on the Damgård–Jurik cryptosystem.
Advances in information theoretic PIR
Achieving information theoretic security requires the assumption that there are multiple non-cooperating servers, each having a copy of the database. Without this assumption, any information-theoretically secure PIR protocol requires an amount of communication that is at least the size of the database n.
Relation to other cryptographic primitives
One-way functions are necessary, but not known to be sufficient, for nontrivial (i.e., with sublinear communication) single database computationally private information retrieval. In fact, such a protocol was proved by G. Di Crescenzo, T. Malkin and R. Ostrovsky in [4] to imply oblivious transfer (see below).
Oblivious transfer, also called symmetric PIR, is PIR with the additional restriction that the user may not learn any item other than the one she requested. It is termed symmetric because both the user and the database have a privacy requirement.
Collision-resistant cryptographic hash functions are implied by any one-round computational PIR scheme, as shown by Ishai, Kushilevitz and Ostrovsky.[6]
See also
References
- A. Beimel, Y. Ishai, E. Kushilevitz, and J.-F. Raymond. Breaking the
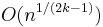 barrier for information-theoretic private information retrieval. Proceedings of the 43nd Annual IEEE Symposium on Foundations of Computer Science, Vancouver, Canada, pages 261-270, 2002.
barrier for information-theoretic private information retrieval. Proceedings of the 43nd Annual IEEE Symposium on Foundations of Computer Science, Vancouver, Canada, pages 261-270, 2002. - Sergey Yekhanin. New locally decodable codes and private information retrieval schemes, ECCC TR06-127, 2006.
Notes
- ^ Benny Chor, Eyal Kushilevitz, Oded Goldreich, Madhu Sudan: Private Information Retrieval. J. ACM 45(6): 965–981 (1998)
- ^ a b c Eyal Kushilevitz, Rafail Ostrovsky: Replication Is Not Needed: Single Database, Computationally-Private Information Retrieval. FOCS 1997: 364–373 (PDF)
- ^ a b Helger Lipmaa: An Oblivious Transfer Protocol with Log-Squared Communication. ISC 2005: 314–328 (PDF)
- ^ Helger Lipmaa: First CPIR Protocol with Data-Dependent Computation. ICISC 2009: 193--210 (PDF)>
- ^ Rafail Ostrovsky, William Skeith. A Survey of Single-Database Private Information Retrieval: Techniques and Applications. Proceedings of the Public Key Cryptography 2007 conference, pp. 393–411. (PKC-2007). (PDF)
- ^ Sufficient Conditions for Collision-Resistant Hashing